前缀和数组与差分数组的实现与应用

前言

这几天学习了数组的一些小技巧，包括前缀和与差分数组，那么下面我将对其展示自己的理解，并实际应用到一些问题中去。

技巧

前缀和数组

前缀和数组是一个基于原数组所生成的新的数组，它的第一个元素是0，后面的第i个元素是原数组区间[0,i-1]的和。

首先先说一下实际应用，例题: 【leetcode 303：区域和检索 - 数组不可变】

给定了一个确定的数组，和n个区间，题目要求求出每个区间内的和。

正常思路使用暴力for循环去做，但是时间复杂度较高，并且题目中的sumRange方法最多可以被调用10^4次，那么效率就非常低了，有没有一种方法能够降低时间复杂度呢？没错，就是使用我们刚刚提到的前缀和数组。

对于一个数组，我要求出其区间[i,j]的和，本质相当于计算前缀和数组的第j+1个元素和第i个元素的差，为什么呢，我们慢慢来分析，我们命名前缀和数组为preSum。

1.preSum[j+1]代表原数组区间[0,j]的和。
2.preSum[i]代表原数组区间[0,i-1]的和。
3.那么preSum[j+1]-preSum[i]就相当于原数组区间[i,j]的和了。

如此，我们思路已经非常清晰了，那么我们用代码来实现一下题解：

class NumArray {
    // 前缀和数组
    private int[] preSum;

    /* 输入一个数组，构造前缀和 */
    public NumArray(int[] nums) {
        // preSum[0] = 0，便于计算累加和
        preSum = new int[nums.length + 1];
        // 计算 nums 的累加和
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    /* 查询闭区间 [left, right] 的累加和 */
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}

至此，对于一维数组的前缀和我们已经很清楚了，那么再提升一步，我们来试一下二维数组的前缀和吧！

来看一下题目【leetcode：二维区域和检索 - 矩阵不可变】

如果我们想计算某一矩阵中的和的话，我们可以使用一个巧妙的方法，如下图所示：

这张图写的非常清晰明了

首先我们用一个二维数组preSum用来记录[0,0]到[i,j]的，长度为原数组长度+1，宽度为原数组长度+1，然后我们用双循环去构建这个数组，具体为：
1.起始索引从1开始，因为前缀和数组首元素均为0
2.要计算[0,0]到[i,j]的和，我们可以使用[0,0]到[i-1,j]的和加上[0,0]到[i,j-1]的和，再加上matrix[i-1][j-1]，就已经覆盖了这整个区域了
3.由于有一部分是重叠的，即[0,0]到[i-1,j-1]，我们再把它减去即可
代码如下：

int m = matrix.length, n = matrix[0].length;
if (m == 0 || n == 0) return;
// 构造前缀和矩阵
preSum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
    for (int j = 1; j <= n; j++) {
        // 计算每个矩阵 [0, 0, i, j] 的元素和
        preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
    }
}

好，现在我们已经把原数组的前缀和数组算好了，我们现在要算[x1,y1]到[x2,y2]的和，我一下说不清楚，和上面原理一样，放一张图你就明白了

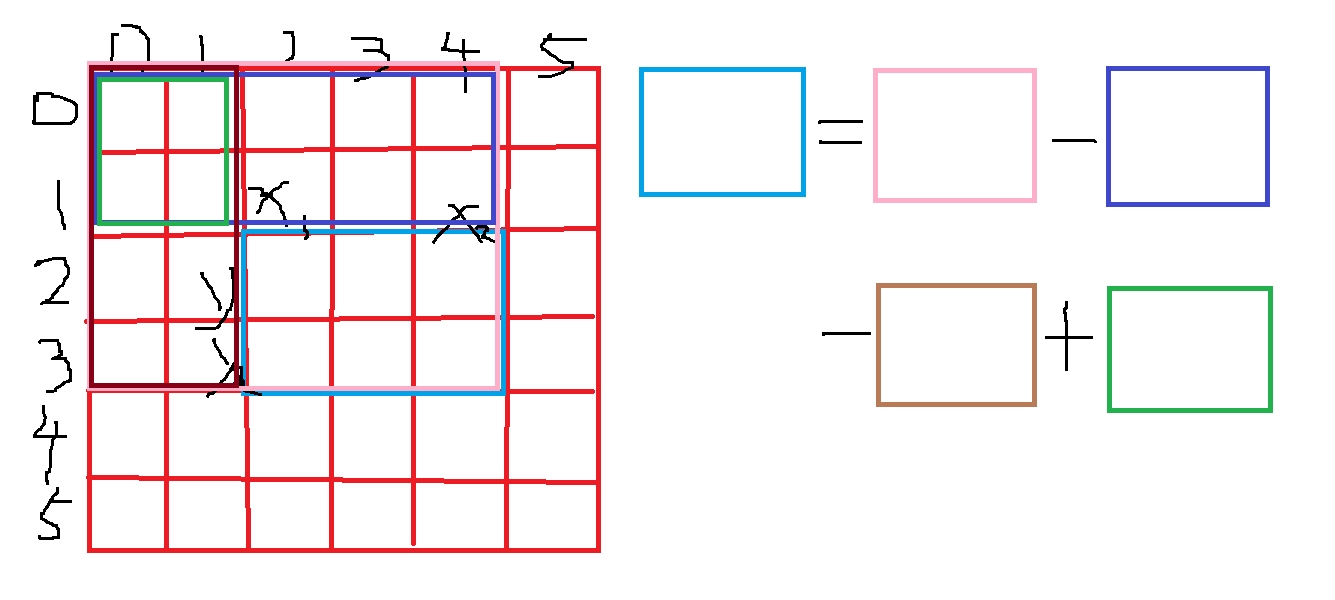
其实原理就是将一个和矩阵的和拆分成从起始点求和的多个矩阵的和差，有如此思路，我们就可以把完整代码写出来了：

class NumMatrix {
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    private int[][] preSum;
    
    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        if (m == 0 || n == 0) return;
        // 构造前缀和矩阵
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 计算每个矩阵 [0, 0, i, j] 的元素和
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // 计算子矩阵 [x1, y1, x2, y2] 的元素和
    public int sumRegion(int x1, int y1, int x2, int y2) {
        // 目标矩阵之和由四个相邻矩阵运算获得
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
}

至此，前缀和已经理解完毕

差分数组

接下来我们看一下差分数组，他和前缀和数组的思想非常相似，所以我才会拿到一起来总结，前缀和是在多次求某个区间的和时，能够大幅降低时间复杂度，而差分数组则常用来对某一区间的元素进行加减，正常我们对一个数组中的指定区间去加减，那么一定要遍历一下，时间复杂度较高，那么我们使用差分数组，就可以很好的解决这个问题了。

差分数组是一种用于处理数组元素变化的技术。它通常用于在数组中高效地执行一系列更新操作，而无需修改整个数组。

差分数组的基本思想是，对于给定数组 arr，创建一个新数组 diff，其中 diff[i] 表示 arr[i] - arr[i-1]。换句话说，diff 中的每个元素都表示原始数组相邻元素之间的差异。

通过使用差分数组，可以在原始数组上进行高效的更新操作。例如，如果要将原始数组中某一范围 [start, end] 的元素都增加某个值 val，只需在差分数组中更新 diff[start] += val 和 diff[end+1] -= val。然后，通过累加差分数组，可以得到更新后的原始数组。

这种方法的优势在于，对于大规模的数组，只需更新少量元素而不是整个数组，从而提高了效率。

下面是一个简单的示例来说明差分数组的基本概念：

假设原始数组是 arr = [1, 2, 3, 2, 1]，那么差分数组为 diff = [1, 1, 1, -1, -1]。如果我们想要将 arr 中索引 1 到 3 的元素都增加 2，只需在差分数组中更新 diff[1] += 2 和 diff[4] -= 2，得到更新后的差分数组 [1, 3, 1, -1, -1]。然后，通过累加差分数组，得到更新后的原始数组 [1, 4, 5, 4, 3]。

知道了差分数组的原理后，我们就可以用代码去实现了：

// 差分数组工具类
class Difference {
    // 差分数组
    private int[] diff;
    
    /* 输入一个初始数组，区间操作将在这个数组上进行 */
    public Difference(int[] nums) {
        assert nums.length > 0;
        diff = new int[nums.length];
        // 根据初始数组构造差分数组
        diff[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            diff[i] = nums[i] - nums[i - 1];
        }
    }

    /* 给闭区间 [i, j] 增加 val（可以是负数）*/
    public void increment(int i, int j, int val) {
        diff[i] += val;
        if (j + 1 < diff.length) {
            diff[j + 1] -= val;
        }
    }

    /* 返回结果数组 */
    public int[] result() {
        int[] res = new int[diff.length];
        // 根据差分数组构造结果数组
        res[0] = diff[0];
        for (int i = 1; i < diff.length; i++) {
            res[i] = res[i - 1] + diff[i];
        }
        return res;
    }
}

最后要生成结果，因为有首元素，和后面元素的差，就可以推导出整个数组。

总结

前缀和（Prefix Sum）：

1.定义： 前缀和是数组中从开头到某个位置的元素之和。
1.表示： 如果原始数组为 arr，则前缀和数组为 prefix_sum，其中 prefix_sum[i+1] 表示 arr[0] + arr[1] + … + arr[i]。
1.应用： 前缀和常用于快速计算数组某一范围内元素的和，通过存储前缀和数组，可以在常数时间内获取任意范围的元素和。

差分数组（Difference Array）：

1.定义： 差分数组是原始数组中相邻元素之间的差值构成的数组。
1.表示： 如果原始数组为 arr，则差分数组为 diff，其中 diff[i] = arr[i] - arr[i-1]。通常将差分数组的第一个元素设为原始数组的第一个元素。
1.应用： 差分数组常用于高效处理数组的修改操作。通过在差分数组中更新某个范围的元素，可以在常数时间内反映这些变化到原始数组中。