前言
今天是打卡学习labuladong的算法笔记第2个月零8天,今天来回顾一下反转链表的各种问题,这篇文章会带你循序渐进的学会各种反转链表的“花招”,从反转整个链表,到反转链表开头n个元素,然后到反转链表一个区间里的元素,再到k个一组反转链表。
复盘
不懂链表的也没有关系,我下面会介绍一些链表,根据这个名字,肯定就可以猜到这是一种像链子一样的数据结构,它同时包含了递归和迭代性质,类型名通常为ListNode,下面是java代码实现:
// 单链表节点的结构
public class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}
好,在了解了基本的链表结构后,我们就可以学习反转链表了(坏笑)
反转整个链表
我们先来看下这道简单题,就是将整个链表反转:【leetcode 206:反转链表】
迭代的方式解决:
class Solution {
public ListNode reverseList(ListNode head) {
// 设置前置节点
ListNode prev = null;
// 设置当前节点
ListNode curr = head;
// 迭代当前节点
while(curr != null) {
// 备份当前节点指向的节点,后面我们需要使当前节点步进,否则无法成功迭代
ListNode next = curr.next;
// 使当前节点指针指向前置节点
curr.next = prev;
// 使前置节点进一位到当前节点
prev = curr;
// 使当前节点进一位到下一个节点,用之前备份过的节点赋给当前节点即可
curr = next;
}
// 迭代过程中,每个节点的指针都会指向前一个节点,进而完成了链表的反转
// 迭代完成后,最后一个节点为prev,那么prev就是反转后的头节点,将其返回即可
return prev;
}
}相比于迭代的方式,递归会更加简洁,这里对于链表,它是符合递归性质的,也就是说它是拥有前序位置和后序位置的
ListNode reverse(ListNode head){
if(head == null || head.next == null) return head;
// 前序
reverse(head.next);
// 后序
}在labuladong这里学习过,这里再和大家复习一下对这两个位置的理解,其实前序位置就是进入这个节点之前的时间节点,后序位置就是离开这个节点之后的时间节点,我们如果想用递归子节点给我们的返回值,那么我们只能用后序位置,前序位置是无法拿到的。
好,这里理解了之后,后面的迭代反转单链表就非常简单了,我们直接来看一下代码把:
// 定义:输入一个单链表头结点,将该链表反转,返回新的头结点
ListNode reverse(ListNode head) {
// 判断当前和下一个节点是否为空,如果为空,说明子节点已经递归完了,一个一个返回即可
if (head == null || head.next == null) {
return head;
}
// 这里我们拿到返回值,也就后面节点反转后的头节点(其实就是原链表的最后一个位置)
// 1->reverse(2->3->4->5)
// 这里就会返回5这个节点
// 1->2<-3<-4<-5
// |
// v
// null
ListNode last = reverse(head.next);
// 那么我们只需要将头节点的下一个节点的指针指向自己,便完成了最后一次反转
// 1<-2<-3<-4<-5
head.next.next = head;
// 这里一定要记得将原头节点的指针指向null,否则就容易
// “Error - Found cycle in the ListNode”
// 产生循环(
head.next = null;
return last;
}有人觉得递归很难理解,其实你们总是一头扎进函数栈里,这样是不对的,一两个还可能想的出来,多了的话,一般人脑子可都承受不了啊(捂脸),正确方法是:
- 明确递归函数的定义,知道如何正确输入,直到使其达到base case
- 在递归的前序或后序位置进行正确的数据更新
- 根据函数的定义返回正确的结果
通过这样分析,不会干烧自己,而且可以清晰的了解递归函数是怎样运作的。
ok,通过反转单个链表后,我们就可以进入到下一小部分了。
反转链表前 N 个节点
在这一部分,我们将实现一个方法,作用是返回反转链表前n个节点的链表的头节点。
函数签名如下:
// 将链表的前 n 个节点反转(n <= 链表长度)
ListNode reverseN(ListNode head, int n)其实和反转单链表相似,只是base case做了改变,以下是代码实现
ListNode successor = null; // 后驱节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// 让反转之后的 head 节点和后面的节点连起来
head.next = successor;
return last;
}- base case:n为1时,我们记录后驱节点,使得能够正确连接两个链表,这里直接返回
head的原因是:n为1,我们只需要反转一个节点 - 接下来进行递归,我们在后序位置使当前头节点的下一个节点指向头节点,这样
last就会返回head后节点反转n-1个节点的链表 - 后一个操作,因为
last是反转后的头节点,也就是原链表的第n个节点,因此我们要反转前n个节点的话,我们只需要将原链表的头节点指向前驱节点successor(即在n为1时保存的节点,用来连接链表),然后只需要返回last即可
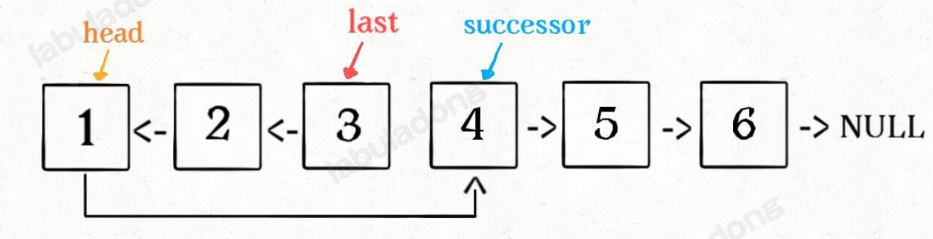
这个也理解好后,我们就可以进入重头戏了。
反转链表的一部分
来看一下这道题:【leetcode 92:反转链表 II】
给一个索引区间 [m, n](索引从 1 开始),仅仅反转区间中的链表元素。
以下为函数签名:
ListNode reverseBetween(ListNode head, int m, int n)考虑这个问题,我们可以先想特殊情况,也就是m==1的时候,我们可以将问题转化为反转链表前n个节点的问题,那么我们直接调用reverseN即可。
好,那么当m!=1时呢,我们如何解决这个问题,利用相对的思想,假设head索引是1,那么我们就要找到第m个节点开始反转,同样假设head.next索引为1,我们就要找到第m-1个节点开始反转……直到m==1时,我们只需要反转前n个即可,我们就又回到了刚才那个问题,只需反转前n个节点就可以了。
好,有了这个思路,我就直接上代码了:
ListNode successor = null; // 后驱节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// 让反转之后的 head 节点和后面的节点连起来
head.next = successor;
return last;
}
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
// 反转前n个节点
return reverseN(head, n);
}
// 前进到反转的起点触发 base case
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}至此,我们反转链表的问题已经大致解决完了,我们再来一道题,继续巩固一下。
K 个一组翻转链表
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
对于这个问题,我们可以先思考一下有没有递归性质,对于一个链表,每k个反转一下,那么链表k个后的链表节点,又可以反转k个,这个就叫递归性质,那么思路就很清晰了:
- 先for循环k次,如果够k次,那么就反转k个,不够,就不变(base case)
- 反转后,将第 k + 1 个元素作为 head 递归调用函数
- 最后,将两次返回结果连接起来即可。
实现代码如下:
/** 反转区间 [a, b) 的元素,注意是左闭右开 */
ListNode reverse(ListNode a, ListNode b) {
ListNode pre, cur, nxt;
pre = null; cur = a; nxt = a;
// while 终止的条件改一下就行了
while (cur != b) {
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
// 返回反转后的头结点
return pre;
}
ListNode reverseKGroup(ListNode head, int k) {
if (head == null) return null;
// 区间 [a, b) 包含 k 个待反转元素
ListNode a, b;
a = b = head;
for (int i = 0; i < k; i++) {
// 不足 k 个,不需要反转,base case
if (b == null) return head;
b = b.next;
}
// 反转前 k 个元素
ListNode newHead = reverse(a, b);
// 递归反转后续链表并连接起来
a.next = reverseKGroup(b, k);
return newHead;
}总结
递归这个东西真的感觉得多多练习,才能熟悉,通过复盘这些题目,旨在提升我的递归能力,加油(