6.28实践学期编程比赛题目的思路以及题解
放麦子
题目描述
你一定听说过这个故事。国王对发明国际象棋的大臣很佩服,问他要什么报酬,大臣说:请在第 1个棋盘格放 1 粒麦子,在第 2 个棋盘格放 2 粒麦子,在第 3个棋盘格放 4粒麦子,在第 4个棋盘格放 8 粒麦子,……后一格的数字是前一格的两倍,直到放完所有棋盘格(国际象棋共有 64格)。 国王以为他只是想要一袋麦子而已,哈哈大笑。 当时的条件下无法准确计算,但估算结果令人吃惊:即使全世界都铺满麦子也不够用! 请你借助计算机准确地计算,到底需要多少粒麦子
思路
这道题目的思路很简单,本质就是一个等比数列求和,首项为1,末项为2^63,公比为2,所以可以直接套用等比数列求和公式,即S = a1 * (1 - q^n) / (1 - q),其中a1为首项,q为公比,n为项数,即S = 1 * (1 - 2^64) / (1 - 2) = 2^64 - 1。
代码
import java.math.BigInteger;
public class Main {
public static void main(String[] args) {
System.out.println(BigInteger.valueOf(2).pow(64).subtract(BigInteger.valueOf(1)));
}
}
答案
18446744073709551615刘谦的魔术
题目描述
2024年央视春节联欢晚会上,刘谦表演了一个基于约瑟夫环问题的魔术。 魔术操作步骤如下: 1、 准备4张不同的扑克牌,随机打乱,即为ABCD; 2、 将4张扑克撕成两半,变成8张,排列为ABCDABCD; 3、 根据名字的长度n,循环n次:将最上面牌放到最下面。假设,n=6,此时,排列为CDABCDAB; 4、 将上面3张牌,放在最后1张牌和第1张(原第4张)之间,此时第1张和最后一张均为B,其他则任意次序,排列为BXXXXXXB; 5、 将第1张放在屁股下面,此时,屁股下为B,剩余排列为XXXXXXB; 6、 南北方人拿上面1或2张牌,随意插入到最后1张之前,排列仍为XXXXXXB; 7、 男生或女生扔掉上面1张或2张,这里以女生为例,排列为XXXXB; 8、 见证奇迹的时刻,循环7次:将最上面牌放到最下面,排列为XXBXX; 9、 好的留下来,将最上面牌放到最下面,排列为XBXXX; 10、 不好的丢出去,扔掉第1张牌,排列为BXXX; 11、 好的留下来,将最上面牌放到最下面,排列为XXXB; 12、 不好的丢出去,扔掉第1张牌,排列为XXB; 13、 好的留下来,将最上面牌放到最下面,排列为XBX; 14、 不好的丢出去,扔掉第1张牌,排列为BX; 15、 好的留下来,将最上面牌放到最下面,排列为XB; 16、 不好的丢出去,扔掉第1张牌,排列为B; 17、 此时,剩下的B和屁股下面的恰好是同一张牌。 假设,4张打乱后的扑克牌,恰好为JQKA。
输入
第一行是整数M,表示有M个问题。 接下来的M行,每行三个整数N、A、X,其中,N表示名字的长度,A是1或2表示南北方,X是1或2表示男女。
输出
输出
每行一个数,与输入相对应的,剩下的那张牌对应的字符。
样例输入
2
2 2 2
3 1 1样例输出
Q
K思路
本题与是南北方,还是男女没有任何关系,我们可以定义一个char数组。
char[] chs = {'J', 'Q', 'K', 'A'};然后对N-1对4取模,从数组中取值即可得到最后剩下的牌。
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
char[] chs = {'J', 'Q', 'K', 'A'};
int M = sc.nextInt();
for (int i = 0; i < M; i++) {
int N = sc.nextInt(), A = sc.nextInt(), X = sc.nextInt();
System.out.println(chs[(N - 1) % 4]);
}
}
}既约分数
问题描述
分子和分母的最大公约数为1的分数,被称为既约分数。例如,8/1、8/3、3/8等等,都是既约分数,请问分子和分母都在[1,2024]之间的既约分数有几个?
思路
直接无脑模拟即可
代码
public class Main {
public static void main(String[] args) {
int cnt = 0;
for(int i=1;i<=2024;i++){
for(int j=1;j<=2024;j++){
if(gcd(i,j) == 1){
cnt++;
}
}
}
System.out.println(cnt);
}
public static int gcd(int x, int y) {
return y == 0 ? x : gcd(y, x % y);
}
}答案
2491447退休次序
题目描述
假设男老师60岁退休,女老师55岁退休。院长想知道老师们的退休次序,请你为下面给出的身份证号码,根据退休的先后重新排序,存在同一天退休的情况时,请将身份证号码字典序小的放在前面
输出
按要求的次序输出,每行一个身份证号码,以及该教师的退休日期,两项信息使用空格分隔
样例输入
2
211402197810030858
420503198307242348样例输出
420503198307242348 20380724
211402197810030858 20381003思路
先对输入的身份证进行处理,将年份加上55或60,定义结构体P,然后使用PriorityQueue进行排序,最后输出即可。
代码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
PriorityQueue<P> pq = new PriorityQueue<>((p1, p2) -> {
if (p1.time == p2.time) {
return p1.id.compareTo(p2.id);
}
return p1.time - p2.time;
});
for (int i = 0; i < N; i++) {
String str = sc.next();
String year = str.substring(6, 10);
int sex = Integer.parseInt(str.substring(16, 17));
StringBuilder sb = new StringBuilder();
int newYear;
if (sex % 2 == 1) {
newYear = Integer.parseInt(year) + 60;
} else {
newYear = Integer.parseInt(year) + 55;
}
sb.append(newYear);
sb.append(str, 10, 14);
pq.add(new P(str, Integer.parseInt(sb.toString())));
}
while (!pq.isEmpty()) {
P p = pq.poll();
System.out.println(p.id + " " + p.time);
}
}
static class P {
String id;
int time;
public P(String id, int time) {
this.id = id;
this.time = time;
}
}
}字符串年号
题目描述
小明用字母A对应数字1 ,B对应 2,以此类推,用Z对应26 。对于27以上的数字,小明用两位或更长位的字符串来对应,例如AA对应27,AB 对应28,AZ对应52,LQ对应329。
输入
一个1~10000之间的整数
输出
对应的字符串
样例输入
2024样例输出
BYV思路
这道题目的思路本质就是一个26进制转换,只不过是从1开始的,所以我们可以先将输入的数减去1,然后不断的对26取余,取余的结果就是对应的字母,然后将余数转换为对应的字母即可。
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
int in = new Scanner(System.in).nextInt();
StringBuilder sb = new StringBuilder();
String str = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
while (in > 0) {
sb.insert(0, str.charAt(--in % 26));
in /= 26;
}
System.out.println(sb);
}
}汉字谜面
题目描述
汉字的字形存在于字库中,即便在今天,16点阵的字库也仍然使用广泛。16点阵的字库把每个汉字看成是16×16个像素信息。并把这些信息记录在字节中。一个字节可以存储8位信息,用32个字节就可以存一个汉字的字形了。 把每个字节转为二进制表示,1表示墨迹,0表示底色。每行2个字节,一共16行,布局是:
第 1 字节,第 2 字节
第 3 字节,第 4 字节
….
第 31 字节, 第 32 字节
这道题目是给你一段多个汉字组成的信息,每个汉字用32个字节表示,这里给出了字节作为有符号整数的值。
题目的要求隐藏在这些信息中。你的任务是复原这些汉字的字形,从中看出题目的要求,并根据要求再编写程序输出答案。
这段信息是(一共 10 个汉字):
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
16 64 16 64 34 68 127 126 66 -124 67 4 66 4 66 -124 126 100 66 36 66 4 66 4 66 4 126 4 66 40 0 16
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
0 -128 64 -128 48 -128 17 8 1 -4 2 8 8 80 16 64 32 64 -32 64 32 -96 32 -96 33 16 34 8 36 14 40 4
4 0 3 0 1 0 0 4 -1 -2 4 0 4 16 7 -8 4 16 4 16 4 16 8 16 8 16 16 16 32 -96 64 64
16 64 20 72 62 -4 73 32 5 16 1 0 63 -8 1 0 -1 -2 0 64 0 80 63 -8 8 64 4 64 1 64 0 -128
0 16 63 -8 1 0 1 0 1 0 1 4 -1 -2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 5 0 2 0
2 0 2 0 7 -16 8 32 24 64 37 -128 2 -128 12 -128 113 -4 2 8 12 16 18 32 33 -64 1 0 14 0 112 0
1 0 1 0 1 0 9 32 9 16 17 12 17 4 33 16 65 16 1 32 1 64 0 -128 1 0 2 0 12 0 112 0
0 0 0 0 7 -16 24 24 48 12 56 12 0 56 0 -32 0 -64 0 -128 0 0 0 0 1 -128 3 -64 1 -128 0 0
思路
因为我们要把每个字节转为二进制表示,1表示墨迹,0表示底色。每行2个字节,一共16行,所以我们可以先将输入的数转为二进制,如果长度不够8,那么就补上前导0,然后遍历一遍构造出的二进制字符串,如果是1就输出*,否则输出空格。
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for (int m = 0; m < 10; m++) {
for (int i = 0; i < 16; i++) {
for (int j = 0; j < 2; j++) {
int n = sc.nextInt();
StringBuilder s = new StringBuilder(Integer.toBinaryString(n));
if (s.length() > 8)
s = new StringBuilder(s.substring(s.length() - 8, s.length()));
while (s.length() < 8) {
s.insert(0, "0");
}
char[] c = s.toString().toCharArray();
for (int k = 0; k < s.length(); k++) {
System.out.print(s.charAt(k) == '1' ? '*' : " ");
}
}
System.out.println();
}
System.out.println();
System.out.println();
}
}
}输出
九的九次方是多少?即387420489。
A和B
题目描述
有两个正整数A和B,A小于B。已知A和B的和X,以及A和B的最小公倍数Y,问A和B是多少?
输入
一个正整数N(N小于50),表示后面有N组数据,接下来的N行,每行两个整数X和Y(0<X,Y<1e9)
输出
输出N行,每行输出与输入相应的A和B,使用空格分隔。
样例输入
2
10 12
8 15
样例输出
4 6
3 5
思路
思路1
暴力做法就是可以先枚举A和B,然后通过给定的X和Y来判断是否满足条件,如果满足条件就输出即可。
但是这样在数据量较大的时候必然会超时,所以我们可以通过数学的方法来解决这个问题。
思路2
我们可以通过A + B = X和lcm(A, B) = Y来解决这个问题,我们可以先求出X和Y的最大公约数gcd,因为gcd(X,Y)和gcd(A,B)是相等的,然后知道Y = A * B / gcd,得A * B = Y * gcd,那么通过两个方程:
A+B=X
A*B=Y*gcd联立得:
A^2 - X * A + Y * gcd = 0这是一个一元二次方程,我们可以通过求根公式来解决这个问题。
A = (X + sqrt(X^2 - 4 * Y * gcd)) / 2代码
暴力做法
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
L:
for (int i = 0; i < N; i++) {
int X = sc.nextInt(), Y = sc.nextInt();
for (int x = 1; x < 1e9; x++) {
for (int y = 1; y < x; y++) {
if (x + y == X && lcm(x, y) == Y) {
System.out.println(y + " " + x);
continue L;
}
}
}
}
}
public static int gcd(int x, int y) {
return y == 0 ? x : gcd(y, x % y);
}
public static int lcm(int x, int y) {
return x * y / gcd(x, y);
}
}数学方法
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
for (int i = 0; i < N; i++) {
int X = sc.nextInt(), Y = sc.nextInt();
int gcd = gcd(X, Y);
int A = (X + (int) Math.sqrt(X * X - 4 * Y * gcd)) / 2;
System.out.println((Y * gcd) / A + " " + A);
}
}
public static int gcd(int x, int y) {
return y == 0 ? x : gcd(y, x % y);
}
}指导小组合并
题目描述
计软学院有n个蓝桥竞赛指导小组,依次编号为1到n。第i个小组的学生数为ti。 由于这些小组的指导内容完全相同,院长认为应该合并成一个大组,统一培训节省成本。于是,院长和这些小组进行沟通,劝说小组和小组合并。 每次沟通院长需要请吃饭,并且一次只能邀请两个小组参加,花费钱数为两个小组的学生数之和乘以100,沟通的效果是两个小组联合成一个小组(学生数为原来两个小组的学生数之和)
输入
输入的第一行包含一个整数N,表示小组的数量。
第二行包含N个正整数,依次表示每个小组的学生数。
其中, 1≤n≤1000,1≤ti≤10000。
输出
输出一个整数,表示最小花费
思路
使用优先级队列(小根堆)来解决这个问题,每次取出两个最小的数,然后将他们相加再放回去,直到队列中只剩下一个数。
代码
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int i = 0; i < N; i++) {
pq.add(sc.nextInt());
}
long sum = 0L;
while (pq.size() > 1) {
int cur = pq.poll();
int cur2 = pq.poll();
sum += (cur+cur2) * 100L;
pq.add(cur+cur2);
}
System.out.println(sum);
}
}差的平方和
题目描述
有N个整数,请计算它们两两之间差的平方的总和
输入
一个正整数N(N小于等于100000),接下来一行有N个绝对值不超过100的整数。
输出
这些数两两之间差的平方的总和
思路
考虑到数据量大,暴力解法的时间复杂度过高(O(N^2)),因此需要优化。可以利用数学推导简化计算。
首先,定义这N个整数为a1, a2, …, aN。
两两之间差的平方的总和可以表示为:
S = ∑∑(ai - aj)² (1 ≤ i < j ≤ N)
展开后,可以得到:
S = ∑∑(ai² - 2ai*aj + aj²) (1 ≤ i < j ≤ N)
因为我们又知道和的平方公式:
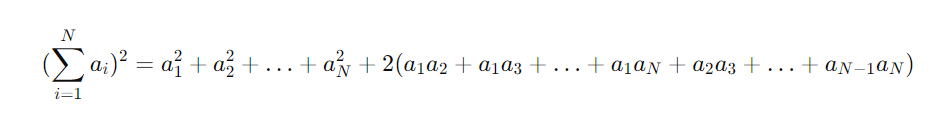
所以我们可以把刚才展开的式子转换为:
S = N * ∑ai² - (∑ai)²
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
long sum = 0;
long sum2 = 0;
for (int i = 0; i < N; i++) {
int num = sc.nextInt();
sum += num;
sum2 += (long) num * num;
}
long result = N * sum2 - sum * sum;
System.out.println(result);
}
}手拉手
题目描述
2个人有4只手,随机从4只手中选两只拉起来(注意:有可能自己左手拉右手),拉上以后不分开,再让未拉起来的两只手拉起来,此时,可能形成一个圈,也可能形成两个圈。形成一个圈的概率是2/3,形成两个圈的概率是1/3。
假设两个人为A、B,四只手AL、AR、BL和BR。第一次随机选两只所有的情况为:(AL、AR)、(AL、BL)、(AL、BR)、(AR、BL)、(AR、BR)和(BL、BR);其中,(AL、AR)和(BL、BR)将形成两个圈,其余4种情况都是形成1个圈。
假设我校有1012名教师,就会有2024只手,现在为了显示大家很团结,随机从这些“手”中找不同的两只拉起来,拉上以后不分开,这样的操作可以进行1012次,问形成几个圈的概率最大?
思路
模拟
因为是填空题,所以我们可以多次模拟这个过程,然后开个数组统计每次形成几个圈,最后看哪个概率最大。
根据大数极限定律,我们这里模拟一万次,然后循环1012次,每次随机选两只手x和y,如果x/2等于y/2,我们认为是一个人,这样自己会形成一个圈,将cnt++,最后将a[cnt]++,最后a数组的最大值就是答案。
模拟开始时一共有0-2023共2024只手,我们可以随机选两只手,下一轮这两个人一共剩下的两只手可以看作是一个人,所以每次选手的范围是2024-2*i。
代码
import java.util.Random;
public class Main {
public static void main(String[] args) {
int[] a = new int[1012];
Random random = new Random();
for (int j = 0; j < 10000; j++) {
int cnt = 0;
int x, y;
for (int i = 0; i < 1012; i++) {
x = random.nextInt(2024 - 2 * i);
do {
y = random.nextInt(2024 - 2 * i);
} while (x == y);
if (x / 2 == y / 2) cnt++;
}
a[cnt]++;
}
for (int i = 0; i < a.length; i++) {
System.out.println(i + " : " + a[i]);
}
}
}输出
0 : 0
1 : 263
2 : 1042
3 : 1916
4 : 2257
5 : 1955
6 : 1395
7 : 676
8 : 313
9 : 119
10 : 46
11 : 13
12 : 3
13 : 1
14 : 1
15 : 0多次运行程序,我们发现4是出现概率最大的,故答案就是4。
动态规划
dp[i][j]表示前i个人形成j个圈的概率,那么我们可以得到状态转移方程:
dp[i][j]=dp[i-1][j-1]/(2*i-1)+dp[i-1][j]*(2*i-2)/(2*i-1);即i个人形成j个圈的概率为i-1个人形成j-1个圈的概率乘以1/2*i-1,加上i-1个人形成j个圈的概率乘以2*i-2/2*i-1。
代码
public class Main {
public static void main(String[] args) {
double[][] dp = new double[1013][1013];
dp[1][1] = 1;
for (int i = 2; i < 1013; i++) {
for (int j = 1; j < 1013; j++) {
dp[i][j] = dp[i - 1][j - 1] / (2 * i - 1) + dp[i - 1][j] / (2 * i - 1) * (2 * i - 2);
}
}
for(int i=0;i<=5;i++){
System.out.println(i+ " " + dp[1012][i]);
}
}
}输出
0 0.0
1 0.027861745925370718
2 0.10443147077807406
3 0.18998976062442263
4 0.22446221467111555
5 0.19426338158655757 可知答案是4。
学生排队
题目描述
有J+R+W名专升本的学生在排队,其中计科专业J名,软工专业R名,网络专业W名。此时,老师发现,从前向后看这一列学生,连续t1个学生同一专业,连续t2个学生同一专业,……,连续tn个学生同一专业。
t1+t2+……+tn等于J+R+W。并且,t1<t2<……<tn。
那么请问在给定J、R、W,并且不区分同一专业学生的情况下,有几种不同的排列方案?
输入
输入第一行是案例数N,接下来每一行有3个整数J、R、W
其中, 0≤J、R、W≤50,0≤J+R+W≤90。
输出
输出N行,每行一个整数,表示与输入相应的答案。
样例输入
2
3 6 0
1 1 1样例输出
3
0思路
我们可以直接使用暴力回溯的方法来解决这个问题,dfs递归函数传入J、R、W、N、X,其中J、R、W分别表示计科、软工、网络的人数,N表示上一次选择的人数,X表示上一次选择专业,如果X为J,那么就不能再选择J,否则会出现连续的J,同理R和W也是如此。
递归边界:当J、R、W都为0的时候,说明已经排完了,那么就可以将答案加一,因为我们排的时候就是按递增的顺序去排的。
然后选择的时候可以尝试,从N+1开始到J、R、W,一一尝试,这里也隐含的去掉了J-i、R-i、W-i小于0的情况。
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
for (int i = 0; i < N; i++) {
int J = sc.nextInt(), R = sc.nextInt(), W = sc.nextInt();
dfs(J, R, W, 0, 'X');
System.out.println(ans);
ans = 0;
}
}
static int ans;
public static void dfs(int J, int R, int W, int N, char X) {
if (J == 0 && R == 0 && W == 0) {
ans++;
return;
}
if (X != 'J') {
for (int i = N + 1; i <= J; i++) {
dfs(J - i, R, W, i, 'J');
}
}
if (X != 'R') {
for (int i = N + 1; i <= R; i++) {
dfs(J, R - i, W, i, 'R');
}
}
if (X != 'W') {
for (int i = N + 1; i <= W; i++) {
dfs(J, R, W - i, i, 'W');
}
}
}
}